Algorithm Analysis | Part 3 - Space Complexity Analysis
@Prajwal
Aug 02, 2022
0 views
4 min read
643 words
This is a 3 Part Series and you're in final part of this series.
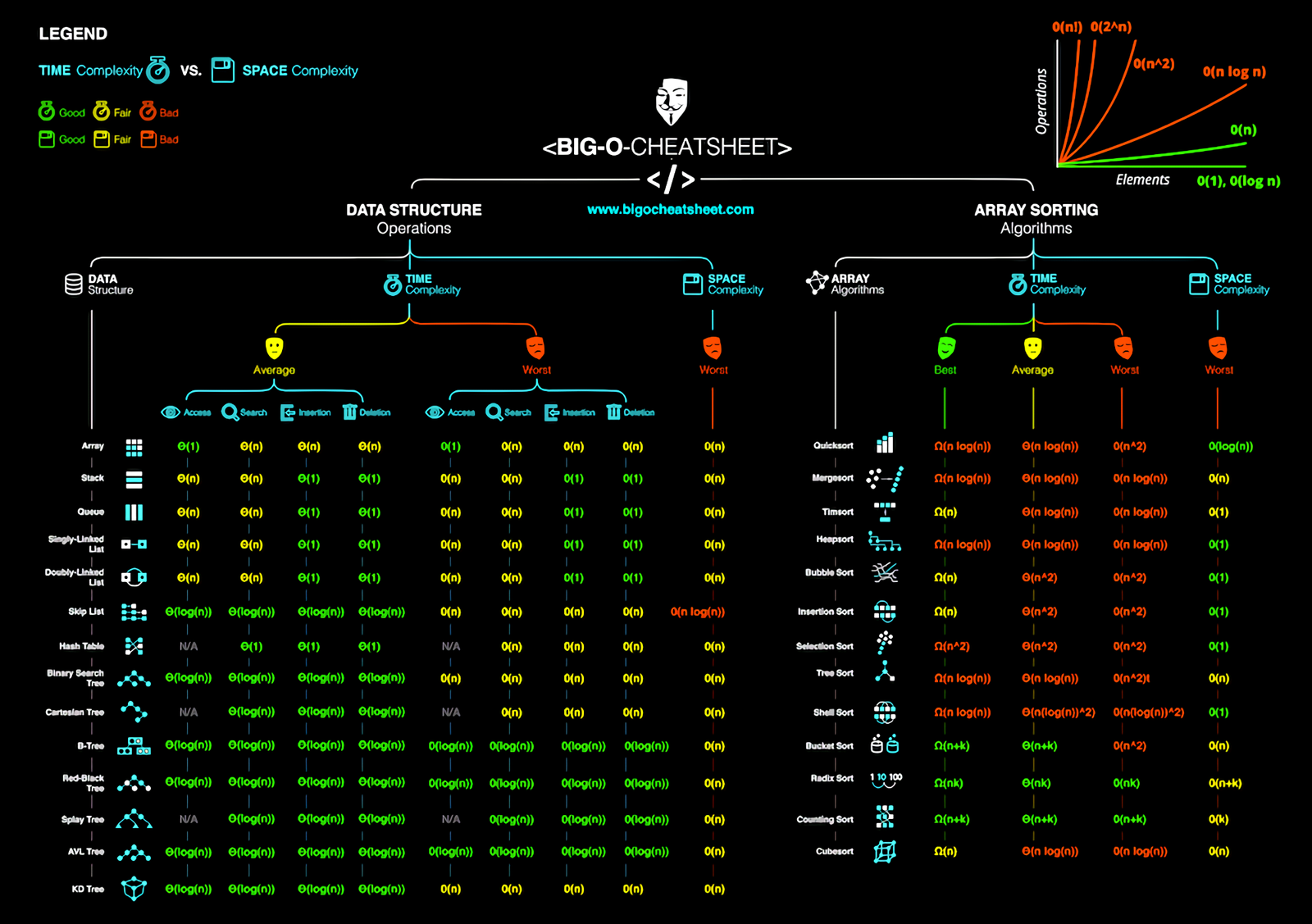
If you're viewing this post for the first time, I highly recommend you to go through the Part 1 & Part 2 of What is Big O Notation And Why Every Programmer Must Know What It Is! series ...
In the previous parts, we discussed the importance of understanding time complexity and how to analyze it. Now, it's time to dive into another critical aspect of algorithm analysis: Space Complexity.
Space complexity measures how much memory or space an algorithm uses relative to its input size. Just like time complexity, understanding space complexity is essential for writing efficient and scalable code. In this blog post, we'll explore what space complexity is, why it matters, and how to analyze it using examples.
What is Space Complexity?#
In simple terms, space complexity refers to the amount of memory an algorithm needs to complete its task as a function of the input size. It helps us understand how much additional memory our algorithm requires beyond the input data.
Space complexity is typically expressed using Big O notation, just like time complexity. Common space complexities include O(1) (constant space), O(n) (linear space), O(n^2) (quadratic space), and more.
Why Does Space Complexity Matter?#
Resource Efficiency: In many cases, memory is a limited resource. Efficient use of memory helps your program run smoothly without running out of memory.
Scalability: As your input size grows, inefficient memory usage can lead to performance problems, including slower execution and potential crashes.
Optimization: Understanding space complexity can lead to more memory-efficient code and help identify opportunities for optimization.
Analyzing Space Complexity#
Let's look at some examples to understand how to analyze space complexity effectively.
Example 1: Constant Space#
def constant_space_example(n): x = 5 return x + n
Analysis: This function uses only a single variable x, regardless of the input size n. Therefore, its space complexity is O(1), indicating constant space usage.
Example 2: Linear Space#
def linear_space_example(n): numbers = [] for i in range(n): numbers.append(i) return numbers
Analysis: In this example, we create a list numbers that grows with the input size n. As n increases, the memory used by the list also increases linearly. Thus, the space complexity is O(n), indicating linear space usage.
Example 3: Quadratic Space#
def quadratic_space_example(n): matrix = [] for i in range(n): row = [] for j in range(n): row.append(i * j) matrix.append(row) return matrix
Analysis: This function constructs a 2D matrix of size n x n, resulting in n^2 elements. As a result, the space complexity is O(n^2), indicating quadratic space usage.
Understanding space complexity is crucial for designing efficient algorithms and writing scalable code. By analyzing space complexity, you can make informed decisions about memory usage, optimize your code, and ensure your programs run smoothly, especially when dealing with large datasets.
In this blog post, we've explored the concept of space complexity and how to analyze it using Big O notation. Armed with this knowledge, you'll be better equipped to write code that not only works but works efficiently, making you a more effective programmer.
Space-Time Trade-offs?#
Space-time trade-offs are decisions made during algorithm design to achieve a balance between the use of memory space and the execution time of an algorithm. In other words, it's about choosing the most efficient algorithm for your specific needs, considering both time and space complexities.
Note: Understanding Big O notation, both for time and space complexity, is a crucial skill for any programmer. It helps you make informed decisions about algorithm and data structure choices, ultimately leading to better code performance and happier users.
Now, go forth and code efficiently! 🚀